Là où tout commence – Fusion au cœur du soleil

Carnets de recherche

Nous et le soleil

Aujourd’hui, vous aviez soif. Vous avez pris un verre d’eau, ou peut-être avez-vous bu directement au robinet. Dans les deux cas, pendant cette action, vous avez utilisé vos bras, probablement vos jambes, certainement vos poumons, et beaucoup d’autres parties de votre corps. Tout cela consomme de l’énergie. Cette énergie provient de la nourriture que vous avez mangée il n’y a pas si longtemps. Imaginons que cette nourriture était des plantes non transformées, d’où vient l’énergie stockée dans ces plantes ?

Vous l’avez probablement deviné, les plantes ont été exposées à la lumière du soleil, et grâce à des réactions biologiques complexes, elles ont stocké l’énergie de la lumière du soleil sous forme de liaisons chimiques. Si vous aviez mangé de la viande, ou une barre de chocolat transformée, ou quoi que ce soit d’autre vraiment, vous devrez juste prolonger un peu la chaîne, mais à un moment donné, vous passerez par l’étape « plante » (la brebis mange de l’herbe, l’herbe est une plante, le chocolat est une plante, le sucre vient de la betterave sucrière, la betterave sucrière est une plante).

Revenons à ce verre d’eau que vous avez eu. Comment se fait-il que l’eau était disponible ? L’eau tombe, c’est la loi de la gravité, alors qu’est-ce qu’elle faisait ailleurs que dans la mer ou dans un lac ? Facile : elle est tombée du ciel et nous, les humains astucieux, l’avons attrapée en chemin pour la stocker, la purifier et la rendre disponible pour que vous puissiez la verser dans un verre. Mais qu’est-ce qu’elle faisait dans le ciel en premier lieu ? La lumière du soleil l’y a mise. Encore merci, soleil.

En réalité, la plupart des choses à la surface de la Terre se déplacent grâce au soleil. Les centrales nucléaires ont un peu changé ce fait, mais surtout pour les choses électriques. Ce ne serait pas exagéré de dire que les centrales nucléaires produisent de l’énergie parce que les humains, qui sont alimentés par le soleil, les ont inventées et les font fonctionner. Les centrales nucléaires ne sont responsables que d’une très petite partie des choses que vous pouvez voir bouger un jour ordinaire. Par conséquent, je dirai avec confiance que la grande majorité de tous les mouvements que vous pouvez observer est en effet rendue possible par le soleil.

Que vous regardiez une feuille doucement soufflée par le vent, un chien courir joyeusement, vos mains faire un peu de vaisselle, ou même une moto rugir en vous dépassant, cela peut être assez impressionnant de réfléchir rapidement à la chaîne d’événements qui relie ces mouvements à l’énergie fournie par le soleil. Bien sûr, la réalité est plus complexe que cette image simpliste et il serait probablement possible de faire une telle déclaration pour d’autres choses que le soleil. Par exemple, les forces électromagnétiques qui maintiennent la matière ensemble sont également importantes. Le soleil n’est qu’un ingrédient. Mais quel ingrédient ! L’énergie du soleil est à tout ce que vous connaissez ce que la farine est à un gâteau. J’aurais dû dire une source de chaleur, je suppose, mais ce serait à peine un ingrédient.

Fusion dans le noyau du soleil

Peut-être pouvez-vous comprendre, alors, pourquoi je trouve ce dessin suivant absolument magnifique :

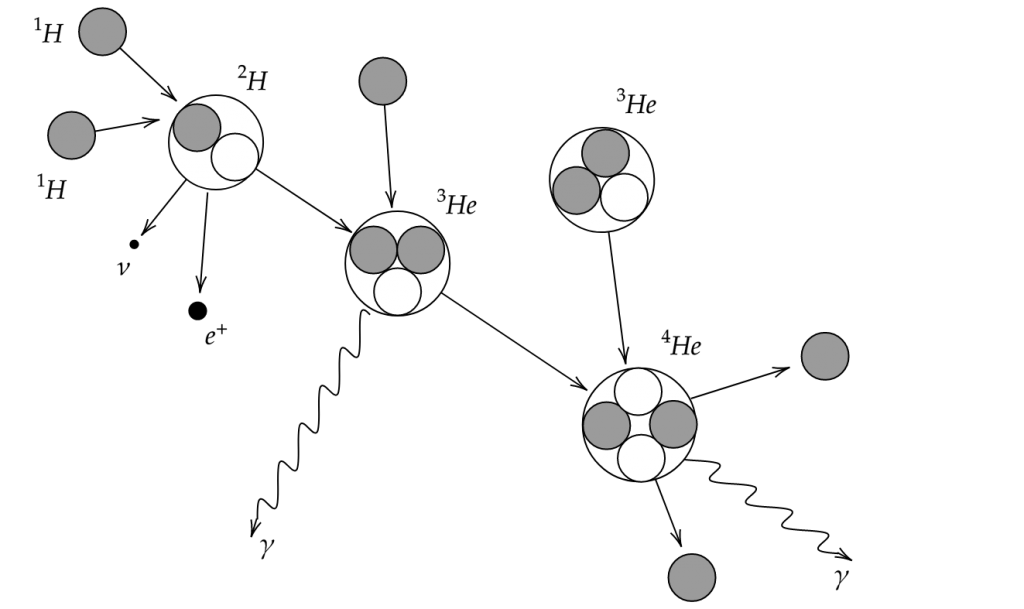
Ou peut-être ne comprenez-vous pas, auquel cas, passons en revue.

Que signifie ce dessin ?
Commençons du côté gauche : le Soleil est principalement composé d’hydrogène (^1 H). Grâce à diverses réactions de fusion, cet hydrogène se transforme en hélium (^4 He), en énergie (sous forme de chaleur et d’énergie cinétique), et en quelques autres choses : (e^+, qui ont une certaine vitesse, et donc une énergie cinétique ; \gamma qui est de la lumière avec beaucoup d’énergie qui rayonnera lentement hors du soleil, et \nu, qui ont également une certaine énergie cinétique mais (presque) ne collident avec rien et la gardent donc pour elles-mêmes.)

La manière dont ce dessin a été réalisé implique un choix artistique, car l’un des ^3He provient de trois autres ^1H, créant ainsi quelques neutrinos, positrons et gammas en cours de route.
La réaction devrait donc vraiment être 4 ^1H \rightarrow ^4He + 2 \nu + 2 e^+ + 2 \gamma.

La question à laquelle je veux répondre ici est : quelle est la puissance délivrée par le soleil ?
Maintenant, 2 \nu + 2 e^+ ont une masse très négligeable par rapport à ^4He, et la plupart de l’énergie qu’ils transportent est cinétique. 2 \gamma sont des photons et n’ont donc pas de masse.

Il est donc habituel d’écrire 4 ^1H \rightarrow ^4He + énergie, et d’essayer de voir combien il y a d' »énergie ».

Utilisons l’équation à peine connue : E= mc^2.

Du côté droit (après le processus de fusion), la masse des particules est m_2 = m(^4He) + 2 m(\nu) + 2 m(e^+), sans masse pour les \gamma car ce sont des photons.
Du côté gauche (avant le processus de fusion), nous avons m_1 = 4 m(^1H).

m(^4He) = 4,00260 u et m(^1H) = 1,00783 u ; avec u = 1,66053 \times 10^{-27} kg. u est appelée la masse atomique.

La masse qui a « disparu » lors de la fusion est \Delta m = m_1 - m_2

Il s’ensuit que l’énergie libérée par la réaction de fusion de 4 atomes de ^1H est \Delta E = \Delta m c^2 = 4,29 \cdot 10^{-12} J

Selon Wikipédia, « le Soleil fusionne 620 millions de tonnes métriques d’hydrogène […] chaque seconde ».
Appelons 620 millions de tonnes métriques d’hydrogène par seconde \dot{M}.

L’énergie libérée par seconde est donc :

P_\odot = \frac{\dot{M}}{4 m(^1H)} \cdot \Delta E

Ce qui donne :

    \[\boxed{P_\odot = 4 \times 10^{26} J/s}\]

Le soleil produit 4 \times 10^{26} joules par seconde. Ce qui équivaut à la puissance nécessaire à 2 \times 10^{23} sèche-cheveux. Ou équivaut à l’explosion imaginaire de 6 \times 10^{12} bombes d’Hiroshima par seconde.

Conclusion

Pourquoi est-ce que cela m’importe personnellement autant, ce nombre ?

Tout d’abord, parce qu’il est absolument gigantesque. Et cela, en soi, c’est assez cool.
Ensuite, parce qu’environ 0,000000000001 \% de cela représente tout ce qui est nécessaire pour alimenter le vent solaire, la météorologie spatiale et mon doctorat : aventures dans le vent solaire.
98 \% de cela est la raison principale pour laquelle nous sommes en vie. C’est aussi à la base d’un projet annexe qui me tient à cœur : géo-ingénierie ?
Enfin, parce que les derniers 2 \% de cette énergie sont emportés par les neutrinos auxquels je ne porte aucune attention personnelle, mais qui sont la raison pour laquelle beaucoup d’autres physiciens se lèvent le matin. Je pense que ce dernier fait est l’une des meilleures preuves possibles de la profondeur, de la complexité et de l’infinitude de la quête de compréhension du monde.

Références :

Physique Spatiale : Une introduction – C.T Russel, J.G. Luhmann, R.J. Strangeway
C’est le livre d’où provient le schéma.

Processus en Astrophysique : La Physique des Phénomènes Astronomiques – H. Bradt
C’est là que j’ai trouvé la formule (1).

Neutrinos Solaires : Où Nous En Sommes, Où Nous Allons – J. N. Bahcall
Cet article de revue peut être un peu vieux, mais il est brillant. Et quel titre !





Bonus :

Je me demandais d’où venait ce nombre \dot{M} = 620 \text{ millions de tonnes par seconde}, et il s’avère qu’en pratique, nous observons la lumière, les neutrinos et le vent solaire émis par le soleil, à partir desquels nous déduisons la puissance P_\odot fournie par le soleil, à partir de laquelle nous déduisons la masse dont le Soleil doit brûler. C’est, pour moi, un peu frustrant, car je préférerais penser de la cause à l’effet plutôt que de l’effet à la cause nécessaire.

Alors je me suis demandé :
(1) sûrement les physiciens des particules doivent savoir, étant donné la densité (disponibilité de « cibles » et « projectiles »)
et la température (énergie des « projectiles »),
à quelle probabilité la réaction de fusion de l’hydrogène a lieu.
(2) en connaissant la densité et la température dans le noyau, vous pourriez être en mesure de déduire la quantité d’hydrogène brûlée par seconde, non ?

(1) Bien sûr qu’ils le font !
Ils donnent même le résultat d’une manière pratique, en puissance par masse de matériau solaire dans lequel les réactions ont lieu (W / kg).
Nous sommes donc en mesure d’écrire, pour des températures et des densités proches de celles du cœur du Soleil :

(1)   \begin{equation*}\epsilon_{pp} = \epsilon_0 X^2 \left( \frac{\rho}{10^5 \text{kg}/\text{m}^3} \right) \left( \frac{T}{10^7 \text{K}} \right)^\beta\end{equation*}



Je dis pratique parce que si nous pouvons déterminer quelle est la masse M_{core} de carburant disponible, nous pouvons écrire : P_\odot = \epsilon_{pp} \times M_{fuel}.
Nous avons écrit, plus tôt, que P_\odot = \frac{\dot{M}}{4 m(^1H)} \cdot \Delta E, donc nous pouvons écrire :

    \[\dot{M} = \frac{ \epsilon_{pp} \times M_{core} 4 m(^1H)}{\Delta E}\]



(2) Puisque le cœur du Soleil a une densité de \rho = 1,5 \times 10^5 \text{kg}/\text{m}^3 et une température de T=1,6 \times 10^7 \text{K}, et que \epsilon_0 \simeq 2 \times 10^{-3} W / kg, X \simeq 0,36 et \beta = 4, vous pouvez trouver :

    \[\epsilon_{pp} = 2,5 \times 10^{-3} \text{W} / {kg}\]



Le cœur a un rayon d’environ R_{core} = 0,2 \times R_\odot avec R_\odot = 6,957 \times 10^8 m le rayon du Soleil. Ce qui signifie qu’il a un volume V_{core} = \frac{4}{3} \pi R_{core}^3. Nous avons déjà la densité \rho donc nous pouvons en déduire la masse disponible de carburant : M_{core}= V_{core} \times \rho.

Et à partir de là, nous pouvons écrire :

    \[\dot{M} = \frac{ \epsilon_{pp} \times V_{core} \times \rho \times 4 m(^1H)}{\Delta E}\]



Et grâce à cela, nous pouvons vaillamment calculer la valeur numérique de \dot{M} :

    \[\boxed{\dot{M} = 6600 \text{ millions de tonnes}}\]



Ce qui est presque exactement dix fois trop grand. Alors que se passe-t-il ? C’est en réalité assez simple de voir où réside le problème :
J’ai supposé une T et \rho constantes dans le cœur solaire, égales à ce qu’elles sont au centre du Soleil, alors qu’en réalité, elles chutent toutes deux significativement à partir du centre. Maintenant, les modèles de l’intérieur du Soleil, même s’ils sont extrêmement bons, nécessitent quelques approximations. Ils doivent également être résolus numériquement, avec d’éventuelles imprécisions en cours de route. Ils peuvent donner le résultat « juste », mais nous savons qu’il est correct uniquement parce que nous avons confiance en nos observations de son effet.

C’est pourquoi l’approche commune et fiable pour arriver à \dot{M} est la première que j’ai mentionnée : procéder de l’effet à la cause nécessaire.

La différence entre la façon dont une découverte est faite et les explications habituelles des enseignants (comme la mienne, si vous oubliez ce « bonus »), est assez courante en physique, et c’est un excellent moyen de réfléchir à des choses de manière nouvelle et différente.
Je crois qu’ils s’enrichissent mutuellement.

Laisser un commentaire