Lasers de Puissance

Physique des plasmas à l'IPP

La limite des Hautes-Densités-d’Energie (HDE)

Le laser apporte autant d’énergie par unité de volume que la cible en contient.
En première approximation, on peut estimer \epsilon, l’énergie par unité de volume dans la cible, à partir de l’énergie de liaisons entre deux molécules de dihydrogène E multipliée par la densité typique d’un solide n.

(1)   \begin{equation*}\begin{split}E & \sim 1 \text{ eV} \sim 10^{-18} \text{ J} \\n & \sim \frac{1}{(1 \text{\AA})^3} \sim 10^{30} \text{ m}^{-3} \\\epsilon & \sim 10^{11} \text{ J.m}^{-3} \\\end{split}\end{equation*}

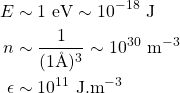
Afin de transporter une telle énergie par unité de volume, un faisceau laser doit avoir une intensité I vérifiant I = \epsilon \cdot c.

On trouve alors que l’intensité typique à partir de laquelle un laser permettra d’accéder au régime HDE est :

(2)   \begin{equation*}\boxed{I^\text{HDE} = 10^{15} \text{ W/cm²}}\end{equation*}

La limite relativiste

Quelle doit-être l’intensité du laser afin d’obtenir une part conséquente d’électrons relativistes ?

Estimons dans un premier temps l’énergie par particule comme : E = m_e c^2.
En prenant la même densité que précédemment, on obtient l’énergie par unité de volume :

(3)   \begin{equation*}\epsilon \sim 10^{-13} \text{ J}\end{equation*}

Cela même à l’intensité typique d’un laser permettant l’accès au régime relativiste :

(4)   \begin{equation*}\boxed{I^\text{relat.} = 10^{21} \text{ W/cm²}}\end{equation*}

L’estimation peut-être revue quelque peu à la baisse si on réalise que 1) les électrons peuvent avoir une énergie de l’ordre d’un dixième de m_e c^2 et être quand même considérés relativistes. 2) Tous les électrons de la cible n’ont pas besoin de devenir relativistes.

La limite ultra-relativiste

Le calcul est le même qu’au dessus, où l’on remplace la masse m_e d’un électron par celle, m_p d’un proton.
On obtient alors :

(5)   \begin{equation*}\boxed{I^\text{ultra-relat.} = 10^{24} \text{ W/cm²}}\end{equation*}

La limite de l’électrodynamique quantique (QED en anglais)

Lorsque le champ magnétique atteint la limite de Schwinger, les collisions entre photons sont tellement énergétiques qu’elles peuvent mener à la création d’une paire électron-positron.
Le champ magnétique de Scwhinger s’écrit :

(6)   \begin{equation*} B = \frac{m_e^2 c^2}{e \hbar} \sim 4 \cdot 10^9 \text{ T} \end{equation*}

On en déduit :

(7)   \begin{equation*}\epsilon \sim \frac{B^2}{\mu_0} \sim 10^{25} \text{ J.m}^{-3}\end{equation*}

Ce qui demande une intensité :

(8)   \begin{equation*}\boxed{I^\text{QED} = 10^{33} \text{ W/cm²}}\end{equation*}


Laisser un commentaire