Turbulence en physique des plasmas

Physique des plasmas à l'IPP

La turbulence est un domaine important de la physique pour plusieurs raisons. Elle contrôle en grande partie les phénomènes de transport dans de nombreux domaines. Elle modifie le type d’énergie contenu dans un système. Et enfin elle pousse la compréhension des équations utilisées pour décrire les fluides. En effet, la turbulence est souvent considérée comme un des derniers problèmes non résolus de la physique classique.

Quand de l’énergie libre est injectée à grande échelle dans un fluide au sein duquel les forces non-linéaires dominent, cette énergie peut être transportée à travers les différentes échelles spatiales du fluide. On appelle ce processus la cascade turbulente. Si le transfert se fait des grandes vers les petites échelles, on parle de cascade directe. Si il se fait des petites échelles vers les grandes, on parle de cascade inverse.

Dans un premier temps, on peut considérer que l’étude de la turbulence est l’étude du transfert de l’énergie d’une échelle à l’autre. On l’associe souvent à l’image des tourbillons :

Des tourbillons de plus en plus petits sont générés à mesure que l’énergie est transportée le long de la cascade turbulente.

Le spectre de Kolmogorov

Dans un soucis de simplicité, considérons ici un fluide dont l’énergie est principalement cinétique. Appelons \varepsilon le taux de transfert de l’énergie d’une échelle à l’autre. On fait l’hypothèse que \varepsilon ne dépend pas de l’échelle considérée. Une première approche phénoménologique pour estimer \varepsilon est de considérer que le temps \tau_{tr} qu’il faut pour que l’énergie cinétique u^2_l d’un tourbillon soit transférée à l’échelle « suivante », est le temps qu’il faut à ce même tourbillon pour tourner sur lui même :

(1)   \begin{equation*}\varepsilon \sim \frac{u^2_l}{\tau_{tr}} \sim \frac{u^2_l}{l / u_l} \sim \frac{u^3_l}{l}\end{equation*}

Attachons nous maintenant à déterminer la forme du spectre en énergie par nombre d’onde, E(k) en fonction du nombre d’onde k = 2 \pi / l. Ceci est important car relativement facile à déterminer à partir d’observations : il suffit de faire la transformée de Fourier du signal. On peut ainsi tester nos hypothèses de départ. On peut estimer, toujours avec notre hypothèse initiale que l’énergie à l’échelle l est principalement l’énergie cinétique des tourbillons de taille l, E(k) k \sim u_l^2. D’après notre équation précédente pour \varepsilon, on a alors :

(2)   \begin{equation*}E(k) k \sim u_l^2 \sim (\varepsilon l)^{2/3} \sim \varepsilon^{2/3} k^{-2/3}\end{equation*}

Ce qui nous permet de conclure que l’énergie spectrale varie avec k selon la loi suivante :

(3)   \begin{equation*}E(k) \propto k^{-5/3} \simeq k^{-1,66}\end{equation*}

L’image suivante est obtenu en prenant la transformée de Fourier du champ magnétique et de la vitesse du plasma dans le vent solaire, proche de la Terre, pendant jours consécutifs; ce qui correspond à trois rotations du soleil sur lui-même :

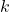Source : Podesta et al. 2007. Spectres du champ magnetique et du champ de vitesse dans le vent solaire, calculés sur un intervalle de 81 jours, ce qui correspond à trois rotations du soleil sur lui-même. Remarque : l’abscisse est ici donnée en Hz. L’hypothèse de Taylor, souvent faite lorsqu’on étudie le vent solaire, stipule que le nombre d’onde k et la fréquence 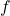f sont directement proportionnels, car ce que mesure un satellite est avant tout une structure quasi-fixe convectée. C’est à dire que l’évolution temporelle des structures contenues dans le vent solaire est très lente par rapport à leur vitesse de déplacement.

Non-linéarité des équations fluides et couplage entre échelles

Supposer l’existence même de \varepsilon suppose que les différentes échelles sont couplées entre elles. Dans les équations fluides comme celle d’Euler, ou à plus forte raison encore celles de la magnétohydrodynamique, de nombreux termes non-linéaires peuvent permettre ce couplage. Pour s’en convaincre, considérons le terme (\bm{u} \cdot \bm{\nabla}) \bm{u} de la partie convective de l’équation d’Euler. Si on imagine qu’il existe une onde monochromatique de fréquence \omega et de nombre k dans le fluide, on pourra exprimer, dans un repère éliminant la phase initiale, u=u_0 \cos(\omega t + k x). Le terme (\bm{u} \cdot \bm{\nabla}) \bm{u} contiendra alors des fréquences plus élevées, en \cos\left( (2 \omega ) t + (2 k) x \right). Ce terme peut alors mener le champ de vitesse à se modifier pour contenir des structures plus fines, qui elles-mêmes donneront lieux à d’autres structures d’encore plus petite taille, etc.

Le nombre de Reynolds dans les plasmas

Le nombre de Reynolds est défini comme le rapport entre les forces inertielles et les forces visqueuses; ou en d’autres termes, on l’obtient en divisant le terme convectif \rho (\bm{u} \cdot \bm{\nabla}) \bm{u} par le terme de viscosité \eta \Delta \bm{u} dans l’équation d’Euler. Il peut-être utilisé pour évaluer la dominance ou non des termes non-linéaires dans les équations fluides. En hydrodynamique, il n’existe qu’un seul nombre de Reynolds. En physique des plasmas, on peut introduire le nombre de Reynolds magnétique en comparant le terme d’advection au terme de diffusion dans l’équation d’induction qui gouverne l’évolution du champ magnétique. S’il est très supérieur à 1, il devient possible qu’une cascade turbulente s’initie dans le plasma, à la condition bien sûr que de l’énergie libre y soit présente. De nombreux plasmas étudiés dans les laboratoires de l’Institut Polytechnique de Paris présentent un nombre de Reynolds très important. Le vent solaire et les plasmas de tokamaks sont par exemple turbulents, présentant dans la plupart des cas des nombres de Reynolds de plusieurs milliers, voire centaines de milliers.

La recherche sur la turbulence plasma

Les hypothèses faites plus haut sont toutes questionables, et questionnées. Par exemple, dans le vent solaire, l’énergie cinétique des tourbillons ne représente environ que la moitié de leur énergie, le reste étant sous forme d’énergie magnétique. Bien que les spectres d’énergie magnétique dans le vent solaire suivent remarquablement la loi de Kolmogorov avec en moyenne une pente de 5/3, cette pente peut varier. Les spectres d’énergie cinétique, en revanche, ont plus tendance à montrer une pente de 3/2. Il semble donc qu’il existe un \varepsilon_v pour la cascade d’énergie cinétique, différent d’un \varepsilon_B pour celle d’énergie magnetique. Pourquoi ?

Comment ces deux types d’énergie, qui sont couplées par les équations décrivant les plasmas, interagissent ensemble le long des cascades turbulentes ? L’hypothèse simple que le terme \epsilon ne dépende pas de l’échelle, bien que relativement bien vérifiée sur des gammes étendues d’échelles, n’est pas non plus toujours vraie. Cela amène à des changements de pente autour de fréquences bien précises. Il faut donc écrire \varepsilon(k). Pourquoi exactement ? Une hypothèse implicite dans les calculs introductifs précédents était l’isotropie du fluide; ce qui en présence d’un champ magnétique à grande échelle devient faux. De quelle manière les cascades turbulentes diffèrent dans les directions parallèles et perpendiculaires au champ magnétique moyen ? Comment identifier \varepsilon(k_{||}) et \varepsilon(k_\perp) à partir de données satellites, par exemple ? Que se passe-t-il en « fin » de cascade turbulente, c’est à dire lorsque les échelles considérées deviennent celles des particules individuelles et que l’hypothèse fluide ne tient plus ? En d’autres termes, comment l’énergie turbulente est-elle « dissipée » sous forme de chaleur ou d’accélération de particules individuelles ?

Ces questions sont celles qui découlent directement de la remise en cause des hypothèses introductives présentées plus haut. Cela dit, il en existe bien d’autres concernant divers aspect de la turbulence, comme son rôle sur le transport de matière et de chaleur dans un tokamak, ou à travers les frontières de l’environnement géomagnétique terrestre. Que se passe-t-il si on prend en tient compte du découplage entre ions et électrons ? Quid des ondes gravitationnelles – peuvent-elles « turbuler » elles aussi ?

Ressources et contacts au sein de l’Institut Polytechnique de Paris

L’axe transverse – Turbulence du LPP
Au sein du Laboratoire des Plasmas (LPP), il existe un « axe transverse » qui associe des chercheurs de différentes équipes (plasmas spatiaux, plasmas de fusion, et parfois même plasmas froids) autour du thème commun de la turbulence dans les plasmas.

Dr Fouad Sahraoui est Directeur de Recherches au CNRS. Il mène des études théoriques et observationnelles (données de missions spatiales) sur les plasmas spatiaux (vent solaire et magnétosphères planétaires).
Sa question favorite : Par quels mécanismes l’énergie est t-elle dissipée dans les plasmas turbulents faiblement collisionnels ?
Pr Sébastien Galtier est Professeur et effectue ses recherches au LPP. Il mène des études théoriques sur la turbulence dans le vent solaire, et de manière plus générale dans les fluides non magnétisés, ou l’univers primordial.
Sa question favorite : Quelles sont les lois fondamentales régissant la dynamique de la turbulence ?
Dr Roland Grappin est Astronome au LPP. Il mène des études numériques et théoriques sur la turbulence dans la couronne solaire et le vent solaire.
Sa question favorite :
Özgür D. Gürcan est Chercheur CNRS au LPP. Il étudie la turbulence avec une approche originale dans l’espace de Fourier. Ses recherches sont menées principalement dans le cadre des plasmas de fusion à confinement magnétique.
Sa question favorite :
Dr Pierre Morel est Maître de Conférence et effectue ses recherches au LPP. Il s’intéresse au transport turbulent dans les plasmas de fusion à confinement magnétique.
Sa question favorite :
Dr Pascal Hennequin, est Directrice de Recherche CNRS et effectue ses recherches au LPP. Elle s’intéresse aux questions de transports turbulents dans les plasmas de tokamaks.
Sa question favorite :

One Comment

  1. Pingback: Fusion à confinement magnétique | Clément Moissard

Laisser un commentaire