Idée 3 – Faire parler ses formules

Petit guide de physique pour étudiant semi-sérieux

Fais-tu partie des 98% d’étudiants qui considèrent les formules comme ben… des formules ?
Haha ! Honte sur toi ! Bon plus sérieusement, c’est dommage. C’est tellement plus que ça une formule !
Mais c’est aussi pas grave, parce qu’à la fin de la lecture de ce petit article, ta vision de la physique va changer à jamais ! (Ou peut-être pas, mais j’y crois.)

Prenons, par exemple, un écoulement stationnaire, incompressible, d’un fluide parfait, sur une ligne de courant reliant un point A à un point B. Supposons qu’on cherche la vitesse v_B du fluide en B.

D’après le théorème de Bernoulli (si tu ne connais pas le théorème de Bernoulli, mais que tu sais ce qu’est une vitesse, une pression et la gravité, aucun problème, reste avec moi tu vas comprendre), on a :

(1)   \begin{equation*}\frac{1}{2}\rho v_A^2 + \rho g z_A + P_A = \frac{1}{2} \rho v_B^2 + \rho g z_B + P_B\end{equation*}

et après un peu de calcul :

(2)   \begin{equation*}\boxed{v_B = \sqrt{v_A^2 + 2g(z_A - z_B) + 2\frac{P_A-P_B}{\rho}}}\end{equation*}

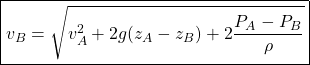
Et ça, c’est logique, compréhensible, et ça fait plaisir, parce que :

  • Plus le fluide va vite en A (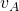v_A grand) [REGARDE LA FORMULE], plus le fluide ira vite en bas (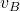v_B grand), et inversement (plus le fluide ira lentement …). [REGARDE LA FORMULE]
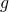  • Plus la différence de hauteur entre A et B est grande (z_A - z_B grand), plus le fluide ira vite en bas, et inversement. [REGARDE LA FORMULE FEIGNASSE !] Et même mieux, si g change, v_B 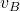change aussi. Donc Bernoulli sur la lune donne des résultats différents que sur Terre, numériquement !
  • Même raisonnement pour la différence de pression (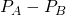P_A - P_B), qui d’ailleurs est modulée par l’inertie du fluide 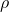\rho. [REGARDE, Bon t’as compris =)]

Je viens de faire « parler la formule ». C’est à dire que j’ai regardé l’effet de chaque terme, et je me suis demandé si ça correspondait à l’image que je me fais de la situation, si c’était logique.

Alors pourquoi est-ce que je te raconte ça ? Pour trois raisons, en fait :

  1. En pratique, c’est une façon efficace de vérifier tes calculs : La formule est logique => tout va probablement bien, la formule est illogique => il faut probablement aller jeter un œil à tes calculs. Je ne connais par exemple aucun autre moyen de corriger facilement des erreurs de signe, ou une faute de calcul bête du style une division qui est devenue une multiplication par mégarde.
  2. C’est « agréable », quand ça marche, de faire le lien entre les formules et le monde réel. Oui je sais, ça demande un peu d’envie de trouver ça agréable… En tout cas, c’est beaucoup plus agréable que de se contenter de manipuler des expressions sans essayer de les « sentir ».
  3. Enfin, plus subtilement, quand la formule paraît illogique ou bizarre, mais que malgré tout elle est juste (ce qui arrive rarement), cela crée une sorte de tension quelque part dans ta tête. Cette tension est une excellente préparation intellectuelle à la compréhension d’un phénomène profond et contre-intuitif. Voire même à la découverte.

Par exemple, la fameuse formule

(3)   \begin{equation*}\boxed{ E=m c^2 }\end{equation*}

:

  • Quand la masse m est grande, l’énergie E est grande. Cette équation représente l’équivalence masse-énergie. Alors Ok, ça me va.
  • Si la vitesse de la lumière était différente, genre plus grande (hypothétiquement hein, c’est quand même une constante fondamentale), alors l’énergie serait plus grande ? HEIN ?! Bah voilà, tension intellectuelle. J’espère que tu reviendras m’expliquer quand ça te paraîtra plus clair =)

5 Comments

  1. Pingback: Idée 5 – Utiliser son imagination – Clément Moissard

  2. Pingback: Idée 6 – La mesure du progrès – Clément Moissard

  4. Bonjour, Je ne suis pas un élève particulièrement doué en physique, mais je pense avoir compris pour c^2 dans l’équation (3). Il faut le voir plutôt comme une valeur limite qu’on ne peut dépasser (« c » est une constante).
    Super article ! Très instructif !

Laisser un commentaire