Magnetically confined fusion

Plasma physics at IPP

Humanity uses approximately 6 \cdot 10^{20} Joules per year. This number has increased from 4 \cdot 10^{19} in 1900 to what it is today [source]. This growth shows no sign of stopping. A significant portion of the energy sources we use has a harmful effect on the environment. Since the second half of the last century, we believe we have found the right idea: magnetic confinement fusion. The fuel: seawater (deuterium) and a little bit of earth (lithium, which can be used to generate tritium) [source]. The waste: no direct products from the fusion reaction, only some of the reactor components that will be activated, but these “wastes” will be manageable and relatively less dangerous compared to the products of fission reactions (Uranium, Plutonium) [source]. The risk of explosion is very low because, unlike fission reactions, fusion reactions cannot run away: they stop on their own.

The idea is relatively simple, elegant, and extreme: let’s do almost the same thing as the core of the sun. In fact, better than the core of the sun because we are less patient. While the sun fuses hydrogen, we will fuse isotopes of hydrogen, which have much higher cross-sections: deuterium (Z = 1, N = 1), and tritium (Z=1, N=2).

(1)   \begin{equation*}\text{D} + \text{T} \rightarrow \text{He} (3.52 \text{ MeV}) + \text{n} (14.06 \text{ MeV})\end{equation*}

The electromagnetic repulsion energy between these two nuclei can be estimated simply by assuming that they must approach each other at 10^{-15} \text{m} to initiate a fusion reaction:

(2)   \begin{equation*}U_{em} = \frac{q q}{4 \pi \epsilon_0 r} \sim 2 \cdot 10^{-13} \text{J} = 1 \text{ MeV}\end{equation*}

We can see that even if we “lost” this energy, the energy balance of the reaction would still be positive. However, the particles would need an energy of 1 \text{MeV}, which corresponds to a temperature of several billion Kelvin. Fortunately, we don’t need to reach such temperatures: on the one hand, because a temperature represents a statistical distribution, and we don’t need all particles to have such kinetic energy, but only a sufficiently large number to produce more energy than we inject to heat the plasma; on the other hand, because the tunneling effect comes to our aid and allows fusion at much lower kinetic energies.

If we take into account their cross-section, and we seek to optimize the efficiency of this reaction, we will rather focus on a plasma of 10 keV \sim 100 million Kelvin. No material on Earth can withstand direct contact with a plasma at such a temperature. So, the challenge is to find an immaterial container: to confine the plasma. This is where the idea of using a toroidal (looping on itself) magnetic field comes into play. We have indeed learned in the early years of university that a charged particle orbits around a magnetic field line:

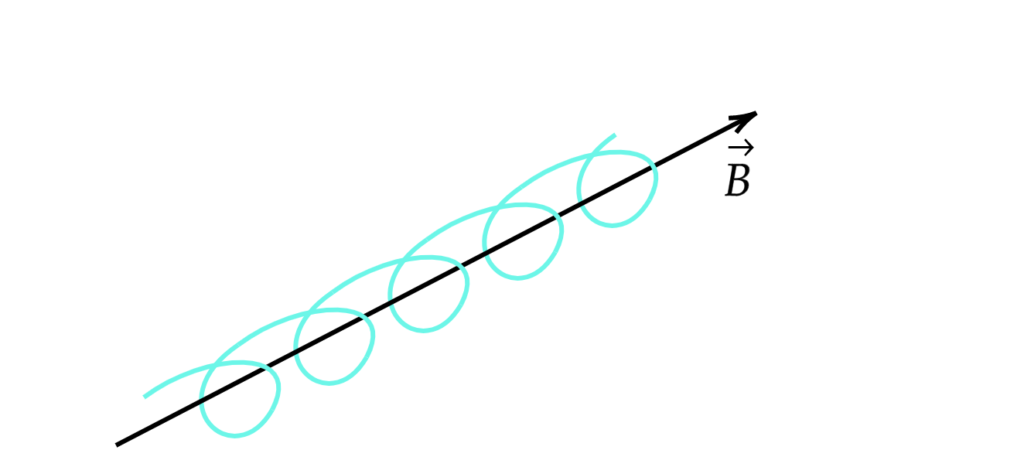
It seems natural to hope to be able to confine one or more charged particles along a magnetic field that loops back on itself.

In order to test this idea, let’s use a relatively simple code (consultable and downloadable here). The motion of a charged particle within a magnetic field is described. We choose a simply toroidal and uniform magnetic field: \bm{B} = B_0 \bm{e}_\theta (please note this is not physical). We hope to see a plasma particle have its trajectory wind around the magnetic field, and thus loop on itself. Here is what we obtain:

The particle escapes. It undergoes a drift motion related to the curvature of the magnetic field. This is an effect described in any introductory book on plasma physics. The general drift formula describing the drift velocity of the guide center (i.e., the center of the quasi-circles that the particle describes around the magnetic field lines) is \bm{v}_\text{drift} = \frac{\bm{F}_c}{qB^2} \times \bm{\bm{B}}. We inject the expression of the centrifugal force: \bm{F}_c = \frac{m v_{||}^2}{R^2}\bm{R}.

This problem was anticipated from the very beginning of research on tokamaks: Just place a poloidal magnetic field. Thus, the particle always drifts upward, but then it falls onto a new field line that tends to gently bring it back down. The following figure, itself highly simplified, gives an idea of the leap in technological and conceptual complexity since our initial naive idea of using a purely toroidal magnetic field.

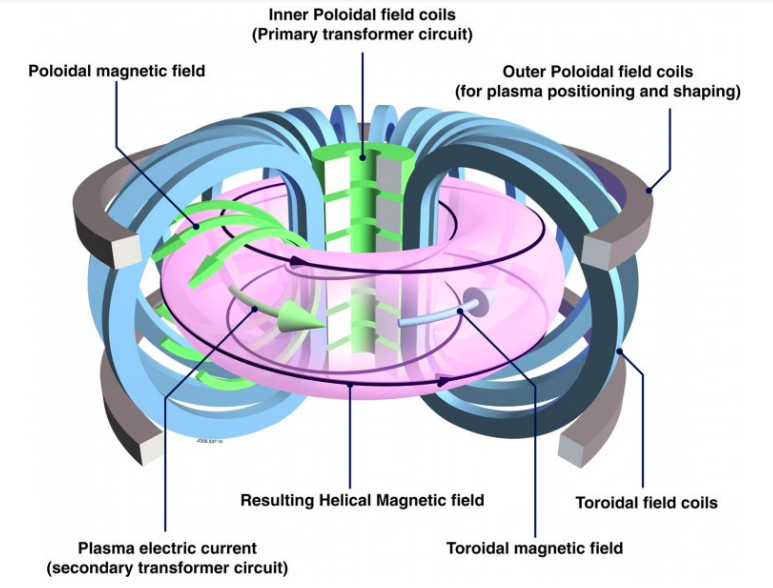
Main elements of a tokamak (credits eurofusion.org, CC-BY 4.0)

This is where the real troubles – and all the interest in research on magnetic confinement fusion – begin. First, this drift is not the only one to act in the tokamak plasma, there are also gradient drifts, because the amplitude of the magnetic field is not uniform. That said, for now, these are just geometry problems. The real difficulty arises when we realize that so far, we have assumed a magnetic field constant in time; whereas in reality the plasma itself modifies the magnetic field. The plasma can be subject to many instabilities, themselves related to various aspects of plasma physics: Instabilities, Magnetic reconnection, Turbulence, etc.

Scientific developments around magnetic confinement fusion are traditionally divided into four major areas:

Plasma-Wall Interaction

For example, the wall is likely to be eroded when in contact with the plasma, and it is possible that some atoms are entrained in the plasma. The atoms constituting the wall are generally much heavier than those in the fusion mixture, and as a result, they radiate much more. Indeed, the Larmor formula, which gives the power radiated by a charged particle of charge Z e during an acceleration phase of amplitude a is written as:

(3)   \begin{equation*}P_L = \frac{Z^2 e^2 a^2}{6 \pi \epsilon_0 c^3}\end{equation*}

If the amount of impurity within the fusion mixture becomes too large, the radiative losses can become so great that igniting the fusion reaction becomes impossible. Some of the problems to be solved are therefore finding the right materials, the right ways to assemble them, and the right shapes for the walls.

Understanding and Controlling Turbulence

A quick estimate of the Reynolds number tells us that turbulence is an important aspect of tokamak plasmas: R_e = \frac{U L}{\nu}

We estimate U \sim \sqrt{k_B T/m} \sim 2 \cdot 10^5 \text{ m/s} (T \sim 10 \text{ keV}) and L \sim 1 \text{ m}.

For \nu we make the simple approximation: \nu = r_L^2/\tau_{ii} where r_L is the Larmor radius and \tau_{ii} is the average time between two collisions between two ions.

(4)   \begin{equation*} $r_L \sim \sqrt{k_B T/m} / (\frac{qB}{m}) \sim 1 \text{ mm}$ (avec $B \sim 5 \text{ T}). \end{equation*}

Obtaining \tau_{ii} requires knowing the mean free path, which can be written as l=\frac{4 \pi \epsilon_0^2 (k_B T)^2}{n e^4 \ln(\Lambda)}. Without going into details, this formula expresses the fact that, on the one hand, the denser a plasma is, the more likely collisions are (which decreases the mean free path), and on the other hand, the hotter a plasma is, the less effective collisions are, which lengthens the mean free path. This comes from the fact that the faster a particle is, the less “easy” it is to change its direction via an electrostatic interaction with another particle. \ln(\Lambda) is a corrective factor that ranges between 5 and 30.

Using this formula, we estimate that the mean free path is about l \sim 3 \cdot 10^3 \text{ m}. We then obtain \tau_{ii} by dividing this mean free path by the average velocity of a particle:

\tau_{ii} \sim l / U \sim 0.003 \text{ s}.

This gives us approximately:

(5)   \begin{equation*}R_e = \frac{U L}{\nu} \sim 10^9\end{equation*}

This unequivocally shows that tokamak plasmas tend to evolve in a highly turbulent regime. For more information on turbulence, see here.

Generation and Control of Continuous Current

Take “Sawtooth crashes” for example:

Ohm’s law tells us that the current is proportional to the electric field, through resistivity \eta:

(6)   \begin{equation*} \bm{J} \propto \frac{1}{\eta} \bm{E}\end{equation*}

Imagine an ideal case (since we seek to reach a stable state) where the electric field \bm{E} is constant. In a plasma, resistivity strongly depends on temperature, according to \eta = \eta_0 T^{-3/2}. Equation (5) tells us that the current will be largest towards the core of the reactor, where the plasma temperature is highest. This tends to give rise to a more significant Joule effect, which raises the temperature. When the current at the center of the reactor becomes too strong, we then expect magnetic reconnection to occur, which destroys (sometimes temporarily, sometimes permanently) the confinement.

Mastering the Dynamics of Suprathermal Populations

The inductive electric field in the toroidal direction tends to accelerate the charged particles (force \frac{e \bm{E}}{m}). These are slowed down by collisions. However, collisions are less and less effective in a plasma as particles go faster (which can be summarized by a force of the type - k \frac{\bm{v}}{v^3}). In short, this comes from the fact that the faster a particle is, the less time it has to interact with the electric field of other particles, and therefore the less time it has to be deflected from its trajectory. Newton’s second law of dynamics then gives us an insight into the problem:

(7)   \begin{equation*} \frac{\text{d} \langle \bm{v} \rangle}{\text{d} t} = - k \frac{\bm{v}}{v^3} - \frac{e \bm{E}}{m}\end{equation*}

There is a speed from which some particles are continuously accelerated by the electric field without being slowed down by collisions.

Research on Magnetic Confinement Fusion

Researchers in magnetic fusion at the Polytechnic Institute of Paris are mainly interested in understanding and controlling turbulence within tokamak plasmas.

How to build a simple model taking into account the rotation of the plasma along the torus?

Resources and Contacts within the Polytechnic Institute of Paris

The Magnetic Fusion Plasmas team at the Laboratory of Plasma Physics
Publications of the Magnetic Fusion Plasmas team at the LPP

Leave a Reply