Power lasers

Plasma physics at IPP

The High-Energy Density (HED) Limit

The laser gives as much energy per unit volume as the target contains. In a nutshell, we can estimate \epsilon, the energy per unit volume in the target, from the binding energy between two dihydrogen molecules, E multiplied by the typical density of a solid, n.

(1)   \begin{equation*}\begin{split}E & \sim 1 \text{ eV} \sim 10^{-18} \text{ J} \\n & \sim \frac{1}{(1 \text{\AA})^3} \sim 10^{30} \text{ m}^{-3} \\\epsilon & \sim 10^{11} \text{ J.m}^{-3} \\\end{split}\end{equation*}

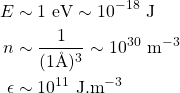
In order to transport such energy per unit volume, a laser beam must have an intensity I verifying I = \epsilon \cdot c.

We then find that the typical intensity at which a laser will allow access to the HDE regime is :

(2)   \begin{equation*}\boxed{I^\text{HDE} = 10^{15} \text{ W/cm²}}\end{equation*}

The relativistic limit

How intense must the laser be in order to obtain a significant proportion of relativistic electrons?

First, let’s estimate the energy per particle as: E = m_e c^2.
Using the same density as above, we obtain the energy per unit volume:

(3)   \begin{equation*}\epsilon{sim 10^{-13} \text{ J}\end{equation*}

This is even at the typical intensity of a laser allowing access to the relativistic regime:

(4)   \begin{equation*}\boxed{I^text{relat.} = 10^{21} \text{ W/cm²}}\end{equation*}

The estimate can be revised downwards somewhat if we realize that 1) electrons can have an energy of the order of a tenth of m_e c^2 and still be considered relativistic. 2) Not all target electrons need to become relativistic.

The ultra-relativistic limit

The calculation is the same as above, where we replace the mass m_e of an electron by the mass m_p of a proton.
The result is :

(5)   \begin{equation*}\boxed{I^\text{ultra-relat.} = 10^{24} \text{ W/cm²}}\end{equation*}

The limit of quantum electrodynamics (QED)

When the magnetic field reaches the Schwinger limit, photon collisions are so energetic that they can lead to the creation of an electron-positron pair.
The Scwhinger magnetic field is written :

(6)   \begin{equation*}B = \frac{m_e^2 c^2}{e \hbar} \sim 4 \cdot 10^9 \text{ T}\end{equation*}

We deduce :

(7)   \begin{equation*}\epsilon \sim \frac{B^2}{\mu_0} \sim 10^{25} \text{ J.m}^{-3}\end{equation*}

This requires an intensity :

(8)   \begin{equation*}\boxed{I^\text{QED} = 10^{33} \text{ W/cm²}}\end{equation*}


Leave a Reply