Turbulence in plasma physics - Clément Moissard

Turbulence is an important domain of physics for several reasons. It largely controls transport phenomena in many fields. It changes the type of energy contained in a system. And finally, it pushes the understanding of the equations used to describe fluids. Indeed, turbulence is often considered one of the last unsolved problems of classical physics.

When free energy is injected on a large scale into a fluid in which nonlinear forces dominate, this energy can be transported across different spatial scales of the fluid. This process is called turbulent cascade. If the transfer occurs from large to small scales, it is called direct cascade. If it occurs from small scales to large, it is called inverse cascade.

Initially, one can consider that the study of turbulence is the study of the transfer of energy from one scale to another. It is often associated with the image of eddies:

*Smaller eddies are generated as energy is transported along the turbulent cascade.*

The Kolmogorov Spectrum

For simplicity, let’s consider a fluid whose energy is primarily kinetic. Let’s call $\varepsilon$ the rate of energy transfer from one scale to another. We assume that $\varepsilon$ does not depend on the scale considered. A first phenomenological approach to estimate $\varepsilon$ is to consider that the time $\tau_{tr}$ it takes for the kinetic energy $u^2_l$ of an eddy to be transferred to the “next” scale is the time it takes for this same eddy to rotate on itself:

(1) $\begin{equation*}\varepsilon \sim \frac{u^2_l}{\tau_{tr}} \sim \frac{u^2_l}{l / u_l} \sim \frac{u^3_l}{l}\end{equation*}$

Now, let’s determine the shape of the energy spectrum by wavenumber, $E(k)$ as a function of the wavenumber $k = 2 \pi / l$ . This is important because it’s relatively easy to determine from observations: just perform the Fourier transform of the signal. We can thus test our initial assumptions. We can estimate, still with our initial assumption, that the energy at scale $l$ is mainly the kinetic energy of eddies of size $l$ , $E(k) k \sim u_l^2$ . According to our previous equation for $\varepsilon$ , we then have:

(2) $\begin{equation*}E(k) k \sim u_l^2 \sim (\varepsilon l)^{2/3} \sim \varepsilon^{2/3} k^{-2/3}\end{equation*}$

This allows us to conclude that the spectral energy varies with $k$ according to the following law:

(3) $\begin{equation*}E(k) \propto k^{-5/3} \simeq k^{-1.66}\end{equation*}$

The following image is obtained by taking the Fourier transform of the magnetic field and the plasma velocity in the solar wind, near Earth, for consecutive days; which corresponds to three rotations of the sun on itself:

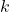**Source: Podesta et al. 2007**. Spectra of the magnetic field and velocity field in the solar wind, calculated over a period of 81 days, corresponding to three rotations of the sun on itself. Note: the abscissa here is given in Hz. The Taylor hypothesis, often made when studying the solar wind, states that the wavenumber $k$ and the frequency 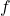$f$ are directly proportional, because what a satellite measures is primarily a quasi-fixed convected structure. That is, the temporal evolution of the structures contained in the solar wind is much slower compared to their displacement speed.

Non-linearity of Fluid Equations and Scale Coupling

Assuming the existence of $\varepsilon$ itself assumes that the different scales are coupled to each other. In fluid equations like Euler’s, or even more so in the equations of magnetohydrodynamics, many nonlinear terms can allow this coupling. To see this, consider the term $(\bm{u} \cdot \bm{\nabla}) \bm{u}$ of the convective part of the Euler equation. If we imagine that there is a monochromatic wave with frequency $\omega$ and wavenumber $k$ in the fluid, we can express, in a reference frame eliminating the initial phase, $u=u_0 \cos(\omega t + k x)$ . The term $(\bm{u} \cdot \bm{\nabla}) \bm{u}$ will then contain higher frequencies, in $\cos\left( (2 \omega ) t + (2 k) x \right)$ . This term can then lead the velocity field to be modified to contain finer structures, which in turn will give rise to other structures of even smaller size, etc.

The Reynolds Number in Plasmas

The Reynolds number is defined as the ratio of inertial forces to viscous forces; or in other words, it is obtained by dividing the convective term $\rho (\bm{u} \cdot \bm{\nabla}) \bm{u}$ by the viscosity term $\eta \Delta \bm{u}$ in the Euler equation. It can be used to assess whether or not the nonlinear terms in the fluid equations dominate. In hydrodynamics, there is only one Reynolds number. In plasma physics, we can introduce the magnetic Reynolds number by comparing the advection term to the diffusion term in the induction equation that governs the evolution of the magnetic field. If it is much greater than 1, it becomes possible for a turbulent cascade to initiate in the plasma, provided of course that free energy is present. Many plasmas studied in the laboratories of the Institut Polytechnique de Paris have a very high Reynolds number. The solar wind and tokamak plasmas are, for example, turbulent, presenting in most cases Reynolds numbers of several thousand, or even hundreds of thousands.

Research on Plasma Turbulence

The assumptions made above are all questionable and questioned. For example, in the solar wind, the kinetic energy of eddies represents only about half of their energy, the rest being in the form of magnetic energy. Although the magnetic energy spectra in the solar wind remarkably follow the Kolmogorov law with an average slope of $5/3$ , this slope can vary. Kinetic energy spectra, on the other hand, tend to show a slope of $3/2$ . So it seems that there is a $\varepsilon_v$ for the cascade of kinetic energy, different from a $\varepsilon_B$ for that of magnetic energy. Why?

How do these two types of energy, which are coupled by the equations describing plasmas, interact along the turbulent cascades? The simple assumption that the term $\epsilon$ does not depend on the scale, although relatively well verified over extended ranges of scales, is also not always true. This leads to changes in slope around very specific frequencies. Therefore, we must write $\varepsilon(k)$ . Why exactly? An implicit assumption in the previous introductory calculations was the isotropy of the fluid; which becomes false in the presence of a large-scale magnetic field. In what way do turbulent cascades differ in the directions parallel and perpendicular to the mean magnetic field? How can we identify $\varepsilon(k_{||})$ and $\varepsilon(k_\perp)$ from satellite data, for example? What happens at the “end” of the turbulent cascade, i.e., when the scales considered become those of individual particles and the fluid assumption no longer holds? In other words, how is turbulent energy “dissipated” as heat or acceleration of individual particles?

These questions are those that directly result from challenging the introductory assumptions presented above. That said, there are many others concerning various aspects of turbulence, such as its role in the transport of matter and heat in a tokamak, or across the boundaries of the Earth’s geomagnetic environment. What happens if we take into account the decoupling between ions and electrons? What about gravitational waves – can they also “turbulate”?

Resources and Contacts at Institut Polytechnique de Paris

The Transverse Axis – Turbulence at LPP
Within the Laboratory of Plasmas (LPP), there exists a “transverse axis” that brings together researchers from different teams (space plasmas, fusion plasmas, and sometimes even cold plasmas) around the common theme of turbulence in plasmas.

Dr. Fouad Sahraoui is a Research Director at CNRS. He conducts theoretical and observational studies (data from space missions) on space plasmas (solar wind and planetary magnetospheres).
His favorite question: By what mechanisms is energy dissipated in weakly collisional turbulent plasmas?
Prof. Sébastien Galtier is a Professor conducting research at LPP. He conducts theoretical studies on turbulence in the solar wind, and more generally in non-magnetized fluids, or the primordial universe.
His favorite question: What are the fundamental laws governing the dynamics of turbulence?
Dr. Roland Grappin is an Astronomer at LPP. He conducts numerical and theoretical studies on turbulence in the solar corona and the solar wind.
His favorite question:
Dr. Özgür D. Gürcan is a CNRS Researcher at LPP. He studies turbulence with an original approach in Fourier space. His research is mainly conducted in the context of magnetically confined fusion plasmas.
His favorite question:
Dr. Pierre Morel is an Associate Professor conducting research at LPP. He is interested in turbulent transport in magnetically confined fusion plasmas.
His favorite question:
Dr. Pascal Hennequin, is a CNRS Research Director conducting research at LPP. She is interested in questions of turbulent transport in tokamak plasmas.
Her favorite question: