Where it all begins – Fusion in the sun’s core

Research notebooks

Us and the sun

Earlier today, you were thirsty. You took a glass of water, or maybe you drank directly from the sink. In either case, during that action, you used your arms, probably your legs, certainly your lungs, and many other parts of your body. All of this consumes energy. This energy comes from food you ate not long ago. Let’s imagine that this food was non-processed plants, where does the energy stored in these plants come from ?

You probably guessed it, the plants were exposed to sunlight, and through complex biological reactions, they stored the energy of sunlight in the form of chemical bonds. If you had meat, or a processed chocolate bar, or anything else really, you do have to make the chain a bit longer, but at one point or another, you’ll go through the “plant” step (sheep eats grass, grass is a plant, chocolate is a plant, sugar comes from sugar beet, sugar beet is a plant).

Going back to that glass of water you had. How come water was available ? Water falls, it’s the law of gravity, so what was it doing anywhere other than in the sea or in a lake? Easy: It fell down from the sky and us clever humans caught it on its way down to store it, purify it and make it available so that you could pour it into a glass. But what was it doing in the sky in the first place? Sunlight put it up there. Again, thanks sun.

Actually, most things on the surface of Earth move thanks to the sun. Nuclear plants have changed that fact a bit, but mostly for electric things. It would not be such a stretch to say that nuclear plants produce energy because humans that are powered by the sun invented them and operate them. Nuclear plants are responsible for only a very small part of the things you can see moving on a regular day. Therefore, I shall confidently state that the vast majority of all the movement you can observe, is indeed made possible by the sun.

Whether you are watching a leaf gently blown by the wind, a dog run happily, your hands doing a bit of washing up, or even a motorbike roar as passes you by, it can be quite awe inspiring to quickly try and think about the chain of events that link those movements to the energy provided by the sun. Of course, the reality is more complex than this simple picture and it would probably be possible to make such a statement for other things than the sun. For example, electromagnetic forces that keep matter holding together are also important. The sun is just an ingredient. But what an ingredient ! Energy from the sun is to everything you know what flour is to a cake. I should have said a source of heat, I suppose, but that would hardly be an ingredient.

Fusion in the sun’s core

Maybe you can understand, then, why I find the following drawing absolutely magnificent:

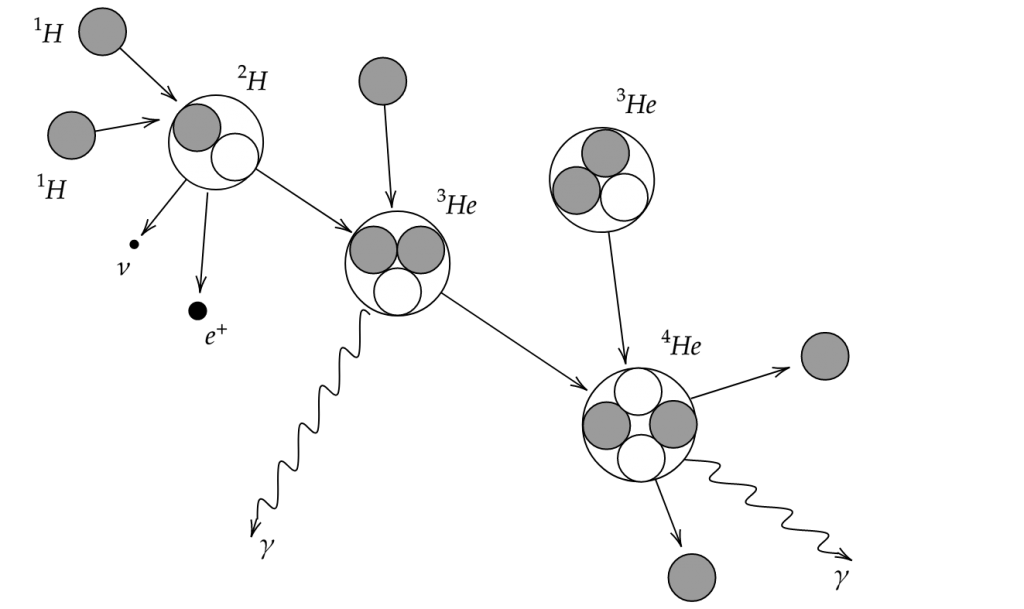
Or maybe you don’t understand, in which case, let us go through it.

What does this drawing mean ?
Let’s start on the left side : the Sun is mostly made of Hydrogen (^1 H). Through diverse fusion reactions, this Hydrogen transforms into Helium (^4 He), energy (heat and kinetic energy), and a few other things: (e^+, which have a certain speed, and therefore a kinetic energy; \gamma which is light with a lot of energy that will slowly radiate out of the sun, and \nu, which also have some kinetic energy but (almost) doesn’t collide with anything and thus keeps it for itself.)

The way this drawing has been made involves an artistic choice, as one of the ^3He came from another three ^1H, creating a few neutrinos, positrons and gamma on the way.
The reaction should, then, really be 4 ^1H \rightarrow ^4He + 2 \nu + 2 e^+ + 2 \gamma.

The question I want to answer here is : what is the power delivered by the sun ?
Now, 2 \nu + 2 e^+ have a very negligible mass compared to ^4He, and most of the energy they carry is kinetic. 2 \gamma are photons so do not have any mass.

It is therfore usual to write 4 ^1H \rightarrow ^4He + energy, and to try and see how much “energy” there is.

Let us make use of the barely heard of equation : E= mc^2.

On the right hand-side (after the fusion process), the mass of the particles is m_2 = m(^4He) + 2 m(\nu) + 2 m(e^+), with no mass for the \gamma because they are photons.
On the left hand-side (before the fusion process), we have m_1 = 4 m(^1H).

m(^4He) = 4.00260 u and m(^1H) = 1.00783 u; with u = 1.66053 \times 10^{-27} kg. u is called the atomic mass.

The mass that “disappeared” during the fusion is \Delta m = m_1 - m_2

And it follows that the energy liberated from the fusion reaction of 4 atoms of ^1H is \Delta E = \Delta m c^2 = 4.29 \cdot 10^{-12} J

According to Wikipedia, “the Sun fuses 620 million metric tons of hydrogen […] each second”.
Let’s name 620 million metric tons of hydrogen per second \dot{M}.

The energy liberated per second is therefore:

P_\odot = \frac{\dot{M}}{4 m(^1H)} \cdot \Delta E

Which gives:

    \[\boxed{P_\odot = 4 \times 10^{26} J/s}\]

The sun produces 4 \times 10^{26} joules per second. Which amounts to the power needed by 2 \times 10^{23} hairdryers. Or is equivalent to the imaginary blowing up of 6 \times 10^{12} Hiroshima bombs per second.

Conclusion

Why do I personnaly care so much about this number ?

Firstly, because it’s absolutely gigantic. And that, in itself, is kind of cool.
Then, because about 0.000000000001 \% of it represents all that is necessary to power the solar wind, space weather, and my PhD: adventures in the solar wind
98 \% of it is the main reason we are alive. It is also at the root of a side-project I care about: geoengineering ?
And finaly because the last 2 \% of this energy are carried away by neutrinos I personnaly don’t care at all about, but are the reason many other physicists wake up in the morning. I think that this last fact is one of the best possible proofs of how deep, complex and endless the pursuit of understanding the world is.

References :

Space Physics : An introduction – C.T Russel, J.G. Luhmann, R.J. Strangeway
This is the book where the diagram comes from.

Astrophysics Processes: The Physics of Astronomical Phenomena – H. Bradt
This is where I found formula (1).

Solar Neutrinos: Where We Are, Where We Are Going – J. N. Bahcall
This review article may be a bit old, but it is brilliant. And what a title !





Bonus:

I was wondering where this number \dot{M} = 620 \text{ million tons per second} comes from, and it turns out that, in practice, we observe the light, neutrino and solar wind emitted by the sun, from which we deduce the power P_\odot delivered by the sun, from which we deduce the mass the Sun needs to be burning. It is, to me, a bit frustrating, as I’d rather think from cause to effect than from effect to necessary cause.

So I wondered:
(1) surely particle physicists must know, given density (availability of “targets” and “projectiles”)
and temperature (energy of “projectiles”),
how likely it is that the reaction of fusion of hydrogen takes place.
(2) knowing the density and temperature in the core, you may be able to deduce the amount of hydrogen burnt per second, right ?

(1) Sure they do !
They even give the result in a convenient way, in power per mass of solar material in which the reactions take place (W / kg).
We are therefore able to write, for temperatures and densities close to the Sun’s core’s :

(1)   \begin{equation*}\epsilon_{pp} = \epsilon_0 X^2 \left( \frac{\rho}{10^5 \text{kg}/\text{m}^3} \right) \left( \frac{T}{10^7 \text{K}} \right)^\beta\end{equation*}



I say convenient because if we can figure out what the mass M_{core} of available fuel is, we can write: P_\odot = \epsilon_{pp} \times M_{fuel}.
We wrote, earlier that P_\odot = \frac{\dot{M}}{4 m(^1H)} \cdot \Delta E, so we can write:

    \[\dot{M} = \frac{ \epsilon_{pp} \times M_{core} 4 m(^1H)}{\Delta E}\]



(2) Since the Sun’s core has a density of \rho = 1.5 \times 10^5 \text{kg}/\text{m}^3 and a temperature of T=1.6 \times 10^7 \text{K}, and since \epsilon_0 \simeq 2 \times 10^{-3} W / kg, X \simeq 0.36 and \beta = 4, you can find:

    \[\epsilon_{pp} = 2.5 \times 10^{-3} \text{W} / {kg}\]



The core has a radius of approximately R_{core} = 0.2 \times R_\odot with R_\odot = 6.957 \times 10^8 m the radius of the Sun. Which means that it has a volume V_{core} = \frac{4}{3} \pi R_{core}^3. We already have the density \rho so we can deduce from it the available mass of fuel : M_{core}= V_{core} \times \rho.

And from that, we can write:

    \[\dot{M} = \frac{ \epsilon_{pp} \times V_{core} \times \rho \times 4 m(^1H)}{\Delta E}\]



And thanks to this, we can bravely compute the numerical value of \dot{M}:

    \[\boxed{\dot{M} = 6600 \text{ million tons}}\]



Which is almost exactly ten times too big. So what is going on? It is actually quite simple to see where the problem lies:
I assumed a constant T and \rho in the Solar core, equal to what they are at the center of the Sun, when in reality, they both drop significantly from the center. Now, the models of the Sun’s interior, even if extremely good, do require a few approximations. They also need to be solved numerically, with potential imprecisions on the way. They may give the “right” result, but we know it is right only because we trust our observations of its effect.

This is why the common, trusted approach to get to \dot{M} is the first one I mentionned: proceeding from effect to necessary cause.

The difference between the way a discovery is made and usual teacher’s explanations (like mine, if you forget this “bonus”), is quite common in physics, and is a great way of thinking about things in novel and different ways.
I believe that they enrich each other.

Leave a Reply